最近Python機械学習を読み進めているのですが、その学習メモです。
前回はこちら
ロジスティック回帰
- 分類モデルの一種
- 実装しやすいが効果があるのは線形分離可能なクラスに対してのみ
- 一対多(OvR)手法に基づいて多クラス分類モデルとして拡張可能
ロジット関数
オッズ比の対数(対数オッズ)
$$ logit(p) = \log\frac{p}{(1-p)} $$
- pは正事象の確率
- 正事象:予測したい事象
- 正事象を\( y=1 \)とすると、ロジット関数を定義できる。
この関数を使って、特徴量の値と対数オッズの間の線形関係を表すことができる
$$ logit(p(y=1|x) = w_0x_0 + w_1x_1 + … + w_mx_m = \sum_{i=0}^mw_ix_i = w^Tx $$
\( logit(p(y=1|x) \)の縦棒は条件付き確率で、発音するときは「given」ということが多いらしい(プログラミングのための確率統計より)
ロジット関数のグラフ表示
import matplotlib.pyplot as plt
import numpy as np
def logit(p):
ones = np.ones(p.size)
return np.log(p / (ones - p))
z = np.arange(0.0001, 0.9999, 0.0001)
phi_z = logit(z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-7, 7)
plt.xlabel('p')
plt.ylabel('$logit(z)$')
# y axis ticks and gridline
plt.yticks(range(-10, 10, 1))
ax = plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
# plt.savefig('./figures/sigmoid.png', dpi=300)
plt.show()
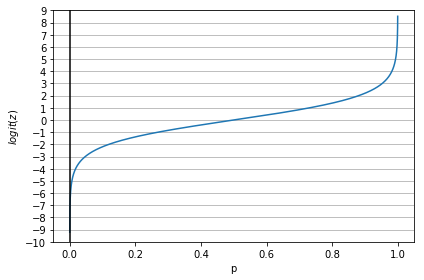
シグモイド関数
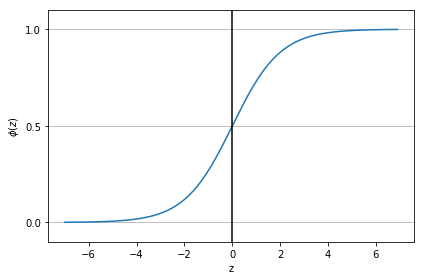
ロジット関数の逆関数。
$$ \phi(z) = \frac{1}{1+e^(-z)} $$
ステップ関数とは異なり緩やかに上昇していくため、例えば結果が降水確率が0.8なら80%である、などの表現が可能になる。
シグモイド関数のグラフ表示
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
# y axis ticks and gridline
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
# plt.savefig('./figures/sigmoid.png', dpi=300)
plt.show()
ロジスティック回帰の重みの学習
尤度L:結果から見たところの条件のもっともらしさ
$$ L(w) = P(y|x;w) = \prod_{i=1}^nP(y^{(i)}|x^{(i)};w) = \prod_{i=1}^n(\phi(z^{(i)}))^{(y^{(i)})}(1-\phi(z^{(i)}))^{1-y^{(i)}} $$
\( P(y|x;w) \)のセミコロン;wはwをパラメータに持つという意味。
対数尤度l:
- アンダーフローの可能性低下
- 積が和に変換されるため加算を用いて微分できるようになる
$$ l(w) = \log L(w) = \sum_{i=1}^n\bigl[(y^{(i)}\log(\phi(z^{(i)})))+({1-y^{(i)})\log(1-\phi(z^{(i)}))}\bigr] $$
上記関数は勾配上昇するので、コスト関数Jとしてはマイナスにする
$$ J(w) = \sum_{i=1}^n\bigl[(-y^{(i)}\log(\phi(z^{(i)})))-({1-y^{(i)})\log(1-\phi(z^{(i)}))}\bigr] $$
1つのサンプルで計算されるコストは、上式から\( \sum \)と\( (i) \)を取って、
$$ J(\phi(z),y;w) = -y\log(\phi(z))-(1-y)\log(1-\phi(z)) $$
上式から、y=0であれば1つ目の項が0になりy=1であれば2つ目の項が0になる。
(mathjaxのせいか正しく表示されない。jupyterだといける。本来は(y=1)のあと折り返し。)
$$ J(\phi(z),y;w) = \begin{cases}
-\log(\phi(z)) & \text (y=1)\
-\log(1-\phi(z)) & \text (y=0)\end{cases} $$
実装
実行に必要なirisデータのダウンロードとプロット関数についてはこちらを参照
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
#print(X_combined_std)
# Pythonでの実装
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰のインスタンスを生成
lr = LogisticRegression(C=1000.0, random_state=0)
lr.fit(X_train_std, y_train)
# 決定境界をプロット
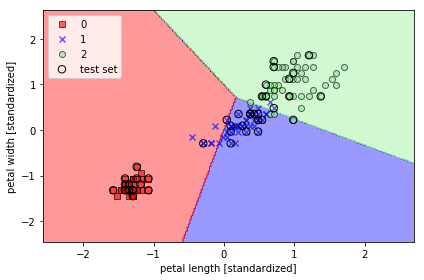
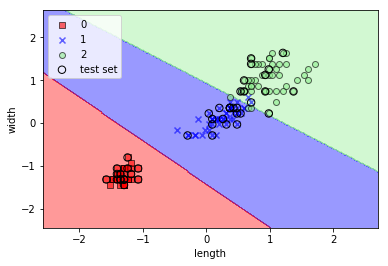
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105, 150))
# ラベル設定
plt.xlabel('petal width(標準化済み)')
# 凡例を設定
plt.legend(loc='upper left')
plt.show()
実行結果
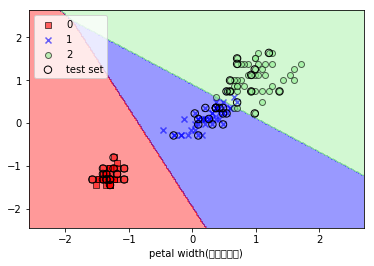
正則化で過学習を防ぐ
- 過学習が発生…高バリアンス
- 学習不足…高バイアス
-
共線性:特徴量の間の相関の高さ
- 正則化:共線性を根拠に過学習を防ぐ。極端なパラメータの重みにペナルティを科す。
L2正則化
- 重みの値の二乗和を正則化項とし、ペナルティ項とする。
- これにより重みの値が大きすぎる場合にペナルティが科され、特定の重みを過剰に重視する過学習を防ぐことに繋がる。
$$ \frac{\lambda}{2}||w||^2 = \frac{\lambda}{2}\sum_{j=1}^m w^2_j $$
\( \lambda \)は正則化パラメータという。
ロジスティック回帰のコスト関数に正則化項をつける
$$ J(w) = \sum_{i=1}^n\bigl[(-y^{(i)}\log(\phi(z^{(i)})))-({1-y^{(i)})\log(1-\phi(z^{(i)}))}\bigr] + \frac{\lambda}{2}||w||^2 $$
正則化パラメータ$ \lambda $の逆数をCとする。
$$ C = \frac{1}{\lambda} $$
これによりコスト関数は以下のように変換される。
$$ J(w) = C\sum_{i=1}^n\bigl[(-y^{(i)}\log(\phi(z^{(i)})))-({1-y^{(i)})\log(1-\phi(z^{(i)}))}\bigr] + \frac{1}{2}||w||^2 $$
パラメータCによる重み係数の変化
weights, params = [], []
# numpy.arange(-5, 5)はだめ。https://github.com/numpy/numpy/issues/8917
for c in range(-5, 5):
lr = LogisticRegression(C=10**c, random_state=0)
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10**c)
weights = np.array(weights)
plt.plot(params, weights[:, 0], label='petal length')
plt.plot(params, weights[:, 1], linestyle='--', label='petal width')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
plt.show()
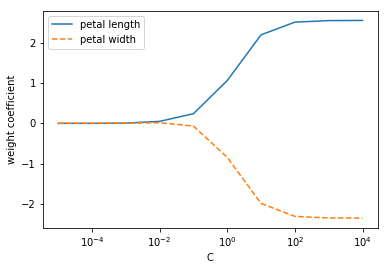
実行結果
- パラメータCが減少して正則化の強さが増すと、重み係数が0に近づく。
コメント