最近Python機械学習を読み進めているのですが、その学習メモです。
前回はこちら
ADALINE
パーセプトロンとの違いは、重みの更新方法
- パーセプトロン:単位ステップ関数
- ADALINE:線形活性化関数 \(\phi(z)\)
目的関数(Objective function) … 学習過程で最適化される関数。多くの場合は コスト関数 (cost function)
コスト関数
誤差平方和(Sum of Squared Error:SSE)
$$ J(w) = \frac{1}{2}\sum_i(y^{(i)}-\phi(z^{(i)}))^2 $$
利点
- 微分可能である
- 凸関数であるため勾配降下法(gradient descent)を用いてコスト関数を最小化する重みを見つけ出すことができる。
勾配降下法を使った重み更新
コスト関数\( J(w) \)の勾配\( \nabla J(w) \)に沿って1ステップ進む
$$ w := w + \Delta w $$
重みの変化である\( \Delta w \)は、負の勾配に学習率\( \eta \)を掛けたもの
$$ \Delta w = -\eta\nabla J(w) $$
勾配計算(偏微分係数)
$$ \begin{align} \frac{\delta J}{\delta w_j} &= \frac{\delta}{\delta w_j}\frac{1}{2}\sum_i(y^{(i)}-\phi(z^{(i)}))^2 \\
&= \frac{1}{2}\frac{\delta}{\delta w_j}\sum_i(y^{(i)}-\phi(z^{(i)}))^2 \\
&= \frac{1}{2}\sum_i2(y^{(i)}-\phi(z^{(i)}))\frac{\delta}{\delta w_j}(y^{(i)}-\phi(z^{(i)})) \\
&= \sum_i(y^{(i)}-\phi(z^{(i)}))\frac{\delta}{\delta w_j}\Bigl( y^{(i)}-\sum_k(w_kx_k^{(i)})\Bigr) \\
&= \sum_i(y^{(i)}-\phi(z^{(i)}))(-x_j^{(i)}) \\
&= -\sum_i(y^{(i)}-\phi(z^{(i)}))x_j^{(i)} \\
\end{align} $$
ADALINEの実装
class AdalineGD(object): """ADAptive LInear NEuron classifier. パラメータ ------------ eta : float 学習率 (0.0~1.0) n_iter : int 繰り返し回数 """ def __init__(self, eta=0.01, n_iter=50): self.eta = eta self.n_iter = n_iter def fit(self, X, y): """ トレーニングデータの学習 """ self.w_ = np.zeros(1 + X.shape[1]) self.cost_ = [] for i in range(self.n_iter): net_input = self.net_input(X) output = self.activation(X) errors = (y - output) self.w_[1:] += self.eta * X.T.dot(errors) self.w_[0] += self.eta * errors.sum() cost = (errors**2).sum() / 2.0 self.cost_.append(cost) return self def net_input(self, X): return np.dot(X, self.w_[1:]) + self.w_[0] def activation(self, X): return self.net_input(X) def predict(self, X): return np.where(self.activation(X) >= 0.0, 1, -1)
学習
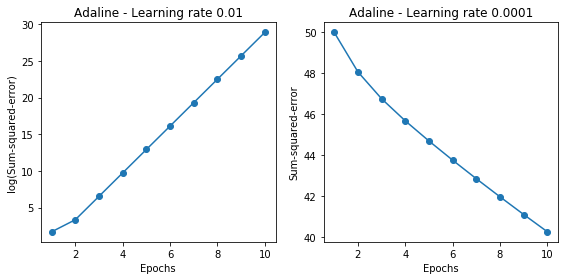
学習結果のプロット
from matplotlib.colors import ListedColormap def plot_decision_regions(X, y, classifier, resolution=0.02): # setup marker generator and color map markers = ('s', 'x', 'o', '^', 'v') colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') cmap = ListedColormap(colors[:len(np.unique(y))]) # plot the decision surface x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) plt.xlim(xx1.min(), xx1.max()) plt.ylim(xx2.min(), xx2.max()) # plot class samples for idx, cl in enumerate(np.unique(y)): plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), edgecolor='black', marker=markers[idx], label=cl)
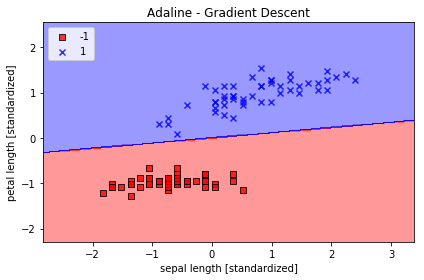
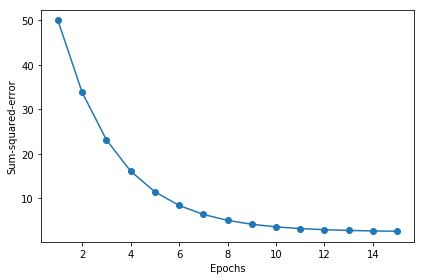
コメントを残す